Capítulo 3 Ordenaciones Directas o Constreñidas
Si bien las técnicas de ordenación indirecta nos permiten descubrir ciertos patrones, no nos permite testar hipótesis y ver las relaciones de esta matriz con otras variables.
Si disponemos de una matriz de variables explicativas es posible utilizar análisis de ordenación constreñidos. De esta forma, esta matriz representa la información que tenemos sobre cada una de las muestras y podemos usarla para predecir los valores de las variables respuesta (la composición de especies).
Al igual que para los análisis de ordenaciones no constreñidas el tipo de ordenación depende de la respuesta que tenemos en las variables (Tabla 3.1 )
| Medidas.de.Similitud | Tipo.de.Ordenación | Tipo.Ordenación.Constreñida |
|---|---|---|
| Respuesta lineal | PCA | RDA (Redundancy Analysis) |
| Respuesta Unimodal | CA/DCA | CCA (Canonical Correspondence Analysis) |
| Bray-Curtis | PcoA/mMDS/nmMDS | PERMANOVA |
Una interesante propiedad de los análisis de ordenación constreñidos es que puedo hacer una ordenación parcial. Esta propiedad me permite evaluar como un grupo de variables pueden influir en mi matriz de respuesta. Podría dividir la información, por ejemplo, en variables ambientales y variables bióticas y ver cuánto explica cada una y cuanto explican en conjunto.
3.1 Realizando una ordenación constreñida
Al igual que en el caso de la ordenación no constreñida debemos decidir el tipo de ordenación constreñida que vamos hacer. En el caso de los datos de Dune sabemos que la respuesta es unimodal por lo que escogeremos un análisis canónico de correspondencias (CCA) para nuestra ordenación constreñida.
Para hacer la ordenación constreñida necesitamos una matriz con variables explicativas, utilizaremos las variables provistas en el paquete vegan denominadas env.env.
data("dune.env") #Llamamos a los datos
ord.cca <- cca(dune~ A1 + Use, data=dune.env)
ord.cca## Call: cca(formula = dune ~ A1 + Use, data = dune.env)
##
## Inertia Proportion Rank
## Total 2.1153 1.0000
## Constrained 0.4724 0.2233 3
## Unconstrained 1.6429 0.7767 16
## Inertia is scaled Chi-square
##
## Eigenvalues for constrained axes:
## CCA1 CCA2 CCA3
## 0.27630 0.14929 0.04683
##
## Eigenvalues for unconstrained axes:
## CA1 CA2 CA3 CA4 CA5 CA6 CA7 CA8 CA9 CA10
## 0.3792 0.3091 0.2093 0.1629 0.1308 0.0965 0.0758 0.0731 0.0483 0.0456
## CA11 CA12 CA13 CA14 CA15 CA16
## 0.0431 0.0237 0.0163 0.0141 0.0108 0.0042Lo que podemos ver es que la variable A1 más Use explican el 22.33% de la variación en los datos.
La decisión de que modelos deberían generar debe responder a una lógica ecológica, así podemos probar como algunas variables juegan o no un rol en la estructura de la comunidad.
Una herramienta que podríamos utilizar para analizar la importancia de cada variable es utilizar la función envfit, esta función permite relacionar la ordenación no constreñida con las variables explicativas y mediante un test de permutación mostrarnos que variables se asocian significativamente con la ordenación.
fitVar <- envfit(ord.ca, dune.env)
fitVar##
## ***VECTORS
##
## CA1 CA2 r2 Pr(>r)
## A1 0.998160 0.060614 0.3104 0.053 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Permutation: free
## Number of permutations: 999
##
## ***FACTORS:
##
## Centroids:
## CA1 CA2
## Moisture1 -0.7484 -0.1423
## Moisture2 -0.4652 -0.2156
## Moisture4 0.1827 -0.7315
## Moisture5 1.1143 0.5708
## ManagementBF -0.7258 -0.1413
## ManagementHF -0.3867 -0.2960
## ManagementNM 0.6517 1.4405
## ManagementSF 0.3376 -0.6761
## UseHayfield -0.2861 0.6488
## UseHaypastu -0.0735 -0.5602
## UsePasture 0.5163 0.0508
## Manure0 0.6517 1.4405
## Manure1 -0.4639 -0.1738
## Manure2 -0.5872 -0.3600
## Manure3 0.5187 -0.3172
## Manure4 -0.2059 -0.8775
##
## Goodness of fit:
## r2 Pr(>r)
## Moisture 0.4113 0.007 **
## Management 0.4441 0.004 **
## Use 0.1845 0.081 .
## Manure 0.4552 0.004 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## Permutation: free
## Number of permutations: 999Podemos utilizar el Goodness of fit para ver cuáles son las variables que ajustan la ordenación y utilizar estas para hacer el modelo constreñido. En este caso utilizaremos Manure y Management.
ord.ccafit <- cca(dune~Manure+Management, data=dune.env)
ord.ccafit## Call: cca(formula = dune ~ Manure + Management, data = dune.env)
##
## Inertia Proportion Rank
## Total 2.1153 1.0000
## Constrained 0.8766 0.4144 6
## Unconstrained 1.2386 0.5856 13
## Inertia is scaled Chi-square
## Some constraints were aliased because they were collinear (redundant)
##
## Eigenvalues for constrained axes:
## CCA1 CCA2 CCA3 CCA4 CCA5 CCA6
## 0.3617 0.2271 0.1454 0.0655 0.0418 0.0353
##
## Eigenvalues for unconstrained axes:
## CA1 CA2 CA3 CA4 CA5 CA6 CA7 CA8 CA9 CA10
## 0.4082 0.1592 0.1493 0.1252 0.0962 0.0774 0.0649 0.0424 0.0382 0.0312
## CA11 CA12 CA13
## 0.0251 0.0121 0.0090Como vemos con este procedimiento subimos al 41% de la varianza explicada.
Podemos utilizar la función anova para evaluar la significancia de cada variable dentro del modelo, de forma separada.
ord.ccaT <- cca(dune~ ., data=dune.env)
anova(ord.ccaT, by="term", permu=1000)## Permutation test for cca under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
##
## Model: cca(formula = dune ~ A1 + Moisture + Management + Use + Manure, data = dune.env)
## Df ChiSquare F Pr(>F)
## A1 1 0.22476 2.5704 0.016 *
## Moisture 3 0.51898 1.9783 0.004 **
## Management 3 0.39543 1.5074 0.060 .
## Use 2 0.10910 0.6238 0.905
## Manure 3 0.25490 0.9717 0.489
## Residual 7 0.61210
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Como vemos esto cambia lo que inicialmente habíamos decidido, esto es debido a que algunas de las variables pueden estar correlacionadas entre ellas.
Bien ahora necesitamos graficar los resultados. Podemos utilizar la función plot e ir graficando cada uno de los componentes (Figura 3.1).
plot(ord.cca, dis="sp", type="n")
points(ord.cca, dis="sites", pch=19, col="grey")
points(ord.cca, display="cn", col="blue", pch=19)
text(ord.cca, dis="sp", cex=0.6)
text(ord.cca, display = "cn", col="blue", cex=0.7)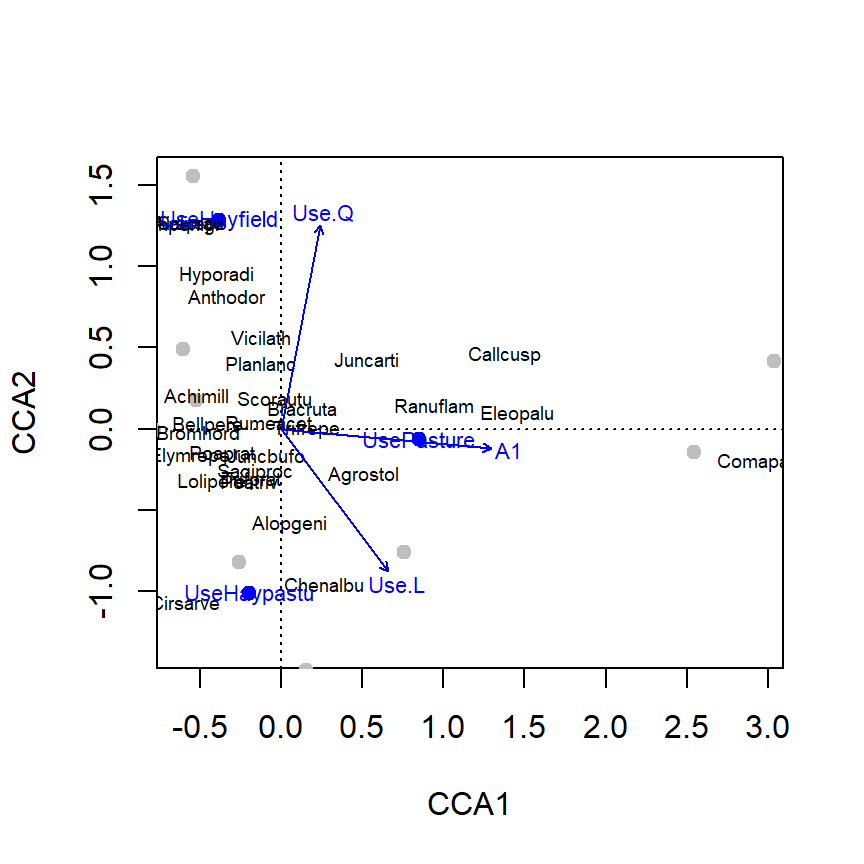
Figure 3.1: Representación gráfica del CCA
Muchas veces uno de los problemas que tenemos para graficar los datos es que los nombres de las especies son muy largos, en estos casos podemos utilizar una función que se denomina make.cepnames la cual permite acortar los nombres.
data(BCI)
names(BCI[1:5])## [1] "Abarema.macradenia" "Vachellia.melanoceras" "Acalypha.diversifolia"
## [4] "Acalypha.macrostachya" "Adelia.triloba"short <- make.cepnames(names(BCI[1:5]))
short## [1] "Abarmacr" "Vachmela" "Acaldive" "Acalmacr" "Adeltril"Existen procedimientos para construir modelos que ahora no tocaremos, puede encontrar más información en Oksanen 2015
Nota: para realizar un permanova debemos utilizar la función adonis. El procedimiento es similar al desarrollo del cca.
3.2 Ejercicio 3: Análisis de Ordenación
Con los datos utilizados para realizar el análisis de aglomerados, vamos a realizar un análisis de ordenación constreñida.
Defina que tipo de ordenación constreñida debe realizar para explicar la variación de los datos de herbáceas.
Realice un análisis para definir las variables que se debería utilizar en el análisis
Ajuste un modelo y defina el porcentaje de variación explicado.
Compara los resultados de la ordenación directa si en vez de transformar los datos corremos los modelos con los datos brutos.
Realice un gráfico del modelo desarrollado.