Capítulo 4 Medidas de Diversidad
Una de las propiedades de las comunidades es la riqueza de especies, sin embargo, esta medida únicamente nos muestra una de las propiedades de la comunidad. Una descripción más completa de la comunidad debería incluir la abundancia de las especies y el número de especies (la riqueza).
Una de las formas más sencillas es desarrollar un modelo de rango de abundancia u obtener una medida de diversidad, un índice de diversidad.
4.1 Modelos de abundancia de especies
El paquete vegan tiene algunas funciones que nos permiten analizar la relación especies-abundancia, algunos de los más utilizados son los modelos para la distribución de la abundancia de especies (rango de especies).
Diagrama de rango de abundancia
El diagrama de rango de abundancia de especies nos permite graficar las abundancias logarítmicas en orden decreciente, o en contra de los rangos de especies (Whittaker, 1965).
La función radfit contiene algunos de los modelos más populares (Wilson, 1991) los cuales utiliza estimadores de máxima verosimilitud. Algunos de los ajustes utilizados son Brokenstick, Preemption, Log-normal, Zipf, Zipf-Mandelbrot. No vamos a profundizar en estos por ahora pero comentaremos como implementarlos en R. Utilizaremos la función radfit para desarrollar el diagrama de rango de abundancia. La función radfit compara los modelos antes enumerados con el fin de evaluar el mejor ajuste, se utiliza el criterio de información de Akaike (AIC) y Bayesianos o de Schwartz (BIC). Estos se basan en log-verosimilitud, pero penalizados por el número de parámetros estimados. La pena por parámetro es 2 en la AIC y log S en BIC.
Vamos a construir dos diagramas para dos parcelas del BCI y para los datos totales de la parcela de 50ha de BCI.
library(vegan)
data(BCI)
pA<- BCI[3,] #escogemos una parcela cualquiera del BCI
pB<- BCI[23,] #otra más
pBCI<- colSums(BCI) #Los datos de todo BCI
RpA<- radfit(pA)
RpB<- radfit(pB)
RpBCI<- radfit(pBCI)
#¿Qué modelo ajusta mejor (tiene menor AIC)?.
#Revise los objetos generados
RpA; RpB; RpBCI##
## RAD models, family poisson
## No. of species 90, total abundance 463
##
## par1 par2 par3 Deviance AIC BIC
## Null 86.1127 347.8863 347.8863
## Preemption 0.052303 58.9295 322.7031 325.2029
## Lognormal 0.94937 1.1957 29.2719 295.0455 300.0451
## Zipf 0.14769 -0.86485 50.1262 315.8997 320.8994
## Mandelbrot 3.9471 -1.705 8.1741 5.7342 273.5077 281.0072##
## RAD models, family poisson
## No. of species 99, total abundance 340
##
## par1 par2 par3 Deviance AIC BIC
## Null 55.4639 322.9662 322.9662
## Preemption 0.038291 53.4573 322.9597 325.5548
## Lognormal 0.7158 1.0327 21.9550 293.4574 298.6476
## Zipf 0.11689 -0.77842 20.0961 291.5984 296.7887
## Mandelbrot 0.50968 -1.1574 3.9378 7.4609 280.9632 288.7486##
## RAD models, family poisson
## No. of species 225, total abundance 21457
##
## par1 par2 par3 Deviance AIC BIC
## Null 10261.14 11387.97 11387.97
## Preemption 0.034063 3788.38 4917.21 4920.63
## Lognormal 3.3569 1.5738 744.30 1875.13 1881.96
## Zipf 0.14679 -0.94912 4335.50 5466.33 5473.16
## Mandelbrot 17.014 -2.0064 15.048 988.02 2120.85 2131.10Como podemos ver el modelo que mejor ajusta (con AIC o BIC más bajo) es, en el caso de la parcela A y B, Mandelbrot y en el caso de los datos completos de la parcela del BCI es Lognormal. Vamos a graficar estas funciones para poder observar las tendencias (Figura 4.1).
par(mfcol=c(1,3))
plot(RpA$models$Mandelbrot, xlim=c(0,250), pch=19, col="black", cex=0.6)
plot(RpB$models$Mandelbrot, xlim=c(0,250), pch=19, col="black", cex=0.6)
plot(RpBCI$models$Lognormal, xlim=c(0,250), pch=19, col="black", cex=0.6)
Figure 4.1: Rangos de abundancia de dos parcelas de BCI y del total de parcelas.
4.2 Índices de Diversidad
Los índices de diversidad son considerados como medidas de la varianza de la distribución de la abundancia de especies. Existen muchos índices desarrollados aunque seguramente el índice de Simpson y de Shannon son los más utilizados.
4.2.1 Índice de Simpson
El índice de Simpson (D) tiene la tendencia de ser más pequeño cuando la comunidad es más diversa. D es interpretado como la probabilidad de un encuentro intraespecífico, esto quiere decir la probabilidad de que si tomas dos individuos al azar de la comunidad ambos sean de la misma especie. Mientras más alta es esta probabilidad menos diversa es la comunidad (sensu Wallace).
Vamos a ejemplificar para entender este concepto con una comunidad completamente equitativa, con 10 especies cada una de las cuales tiene una abundancia de 5.
#Generamos un vector con 10 especies, cada una con 5 individuos
abun<- rep(5,10)
#Sacamos la abundancia relativa
rel<- abun/sum(abun)
rel## [1] 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1A partir de estos datos podemos utilizar el índice de Simpson:
\[ D=\sum_{i=1}^S p_i^2 \]
Donde S es el número de especies y pi es la proporción de cada especie.
#calculamos el índice de Simpson
D<- sum((rel)^2)
D## [1] 0.1Para evidenciar como D (la probabilidad de un encuentro intraespecífico) aumenta cuando la comunidad es menos equitativa piensa en el ejemplo de una comunidad con una especie diez veces más abundante que las demás.
#Generamos un vector con 10 especies, 1 con 50 individuos y el resto con 5 individuos
abun2<- rep(c(50,5),c(1,9))
#Sacamos la abundancia relativa
rel2<- abun2/sum(abun2)
rel2## [1] 0.52631579 0.05263158 0.05263158 0.05263158 0.05263158 0.05263158
## [7] 0.05263158 0.05263158 0.05263158 0.05263158D2<- sum((rel2)^2)
D2;D## [1] 0.3019391## [1] 0.1Dado de que queremos un índice que aumenta con la diversidad en vez de disminuir, sería mejor si podemos interpretar el índice en una forma directa. Entonces es común usar el inverso del índice de Simpson
invD=1-D
invD<- 1-D
invD2<- 1-D2
invD;invD2## [1] 0.9## [1] 0.6980609Como podemos ver ahora la comunidad con una repartición de la abundancia más equitativa (D) tiene un índice más alto (invD) que la comunidad con una especie dominante (D2).
4.2.2 El índice de Shannon
El índice de Shannon H mide más o menos lo mismo que el índice de Simpson, sin embargo, su lógica teórica está basada en teoría informática. Esto hace su interpretación un poco menos intuitiva. Sin ir a más detalle H normalmente toma valores entre 1 y 4.5. Valores encima de 3 son típicamente interpretados como “diversos”. Por razones que no son tan obvias como el caso de Simpson el máximo valor que puede tomar H es el logaritmo de S (número de especies), ln(S). El índice de Shannon-Weaver es expresado como:
\[ H=-\sum_{i=1}^S p_ilog_bp_i \]
Volveremos a utilizar las comunidades que generamos para testar el índice de Shannon con el fin de evaluar su comportamiento.
H<- -sum((rel*(log(rel))))
H2<- -sum((rel2*(log(rel2))))
H;H2## [1] 2.302585## [1] 1.732552Al igual que en el caso de Simpson, la comunidad más diversa es la comunidad con una menor dominancia. En la figura 4.2 vemos como varían los dos índices muestran que la comunidad más dominante representa el 75% de la comunidad equitativa según Shannon, mientras que en Simpson muestra que esta representa el 77%.
##Vamos a generar un gráfico con los dos índices
par(mar=c(2,2,1,1))
div<- c(invD,invD2,H,H2)
names(div)<- c("D","D2","H","H2")
barplot(div, ylim=c(0,3), main="Variación de la diversidad",
cex.main=0.8, cex.axis=0.7, cex.names=0.7)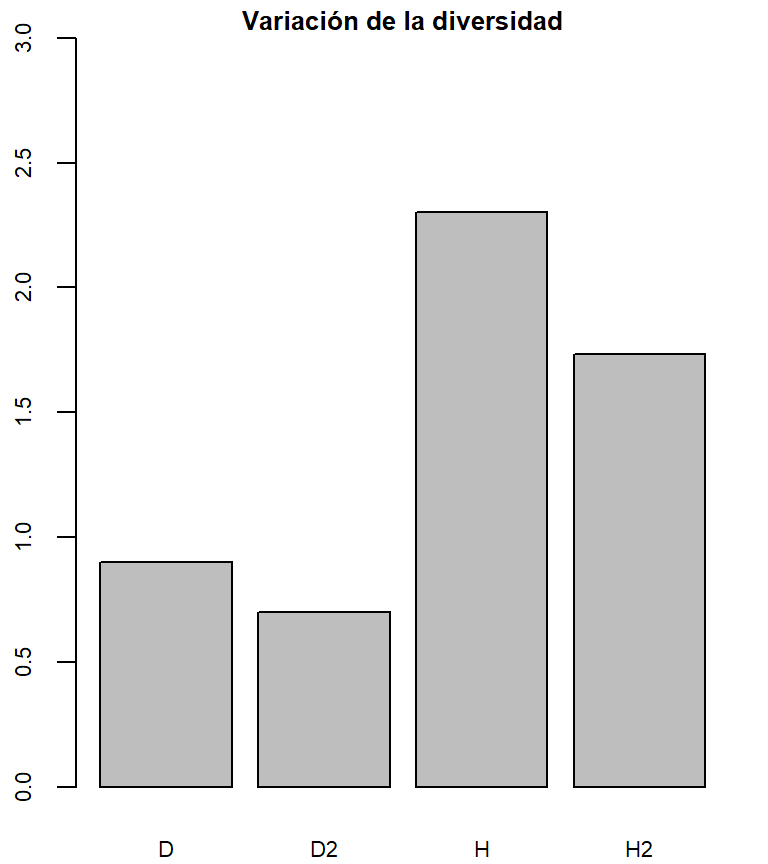
Figure 4.2: índices de diversidad de Simpson (D y D2) y de Shannon (H y H2) de dos comunidades con menor y mayor dominancia respectivamente.
Aunque como vemos es muy sencillo realizar los índices de Shannon y Simpson podemos utilizar la función diversity para calcular los índices.
diversity(abun2, "simpson")## [1] 0.6980609diversity(abun, "simpson")## [1] 0.9diversity(abun, "shannon")## [1] 2.302585diversity(abun2, "shannon")## [1] 1.732552Existen otros índices que pueden ser explorados dentro de la función diversity.