Capítulo 2 Rarefacción

La riqueza es una de las medidas más simples e intuitivas que describen una comunidad, sin embargo, uno de los problemas del uso de esta medida es su dependencia del tamaño muestreal (Magurran 2004), esto implica que la riqueza (y las otras medidas de diversidad) puede verse influida por variaciones en el esfuerzo muestreal. Aunque el diseño experimental está pensado para estandarizar el esfuerzo muestreal, los tamaños finales muestreales difícilmente son iguales.

Un esfuerzo de muestreo desigual puede tener impactos en las medidas de riqueza de especies

— (Magurran 2004)

Esto representa un inconveniente, ya que muestreos en principio del mismo tamaño, podrían capturar números significativamente diferentes de individuos. Pensemos que una red para aves podría capturar 150 individuos en un sitio y 25 en otro. Cuan comparables serían estos datos si sabemos que el tamaño de la muestra influye en la cantidad de especies colectadas.

De esta manera, necesitamos separar dos conceptos distintos, la densidad de especies de la riqueza de especies. Imaginemos dos área cualquiera donde vamos a muestrear la vegetación, estas dos áreas únicamente se diferencian porque en la una existe pastoreo y en la otra no. Vemos que pasa cuando muestreamos cada una de estas comunidades.

#Generamos unas comunidades
pas <- data.frame( sp = paste(rep("sp", 30), 1:30, sep="-"), abun= sample(1:12, 30, replace=TRUE))
pas1 <- matrix(0, 40,30)
colnames(pas1) <- pas[,1]
for(i in 1:30){
pas1[,i] <- c(rep(1, pas[i,2]), rep(0, 40-pas[i,2]))
}
pas1 <- pas1[order(sample(1:40, 30)), ]

npas <- data.frame( sp = paste(rep("sp", 30), 1:30, sep="-"), abun= sample(30:40, 30, replace=TRUE))
npas1 <- matrix(0, 40,30)
colnames(npas1) <- npas[,1]
for(i in 1:30){
npas1[,i] <- c(rep(1, npas[i,2]), rep(0, 40-npas[i,2]))
}
npas1 <- npas1[order(sample(1:20, 20)), ]

#Ahora las muestreamos
m_pas <- matrix(0,3,30)
colnames(m_pas) <- colnames(pas1)
m_pas[1,] <- sample(pas1, 30)
m_pas[2,] <- sample(pas1, 30)
m_pas[3,] <- sample(pas1, 30)

m_npas <- matrix(0,3,30)
colnames(m_npas) <- colnames(pas1)
m_npas[1,] <- sample(npas1, 30)
m_npas[2,] <- sample(npas1, 30)
m_npas[3,] <- sample(npas1, 30)

#Calculamos la riqueza de las muestras
specnumber(colSums(m_pas)) #Pastoreado

## [1] 13

specnumber(colSums(m_npas))#No Pastoreado

## [1] 30

Como vemos por puro azar la diversidad es mucho mayor en las parcelas no pastoreadas, pero realmente hay mayor diversidad? Obtengamos la diversidad total de cada comunidad.

specnumber(colSums(pas1))#Pastoreado

## [1] 30

specnumber(colSums(npas1))#No Pastoreado

## [1] 30

Efectivamente la riqueza es la misma, el único problema es que en la zona pastoreada tiene una menor abundancia lo que origina una menor densidad de especies, sin embargo, no hay un efecto sobre la riqueza de especies.

Algunos índices basados en la riqueza como el de Margalef y Menhinick han sido propuestos para minimizar estos efectos, pero este ajuste ha mostrado ser insuficiente (Magurran, 2004). Una solución más aceptada a este problema es realizar una rarefacción, que es una forma de remuestrear las parcelas en función de un tamaño de muestra único para todas las parcelas.

Específicamente la rarefacción es el proceso de generación de la relación entre el número de especies vs el número de individuos en una o más muestras (Stevens 2009). Esta corrección por el número de individuos nos permite la comparación directa de la riqueza de dos muestras que inicialmente tenían diferente tamaño.

Para poder abordar estos temas utilizaremos la función rarefy del paquete vegan. La función rarefy arroja como resultado la riqueza de especies esperada en un determinado tamaño de muestra.

La rarefacción puede realizarse solamente con auténticos datos de conteos. La función rarefy se basa en la formulación de Hurlbert (1971), y los errores estándar sobre Heck et al. (1975).

Hurlbert (1971) propone la rarefacción como:

\[S_n= \sum_{i=1}^S (1-q_i)\]

Donde; \(q_i= \frac{(\frac{n-x_i}{n})}{(\frac{N}{n})}\) que representa las probabilidades de que las especies i no ocurra en una muestra de tamaño n, \(x_i\) es el conteo de i especies y \((\frac{N}{n})\) es el coeficiente binomial o el número de formas en las que puede elegir n de N

En otras palabras la rarefacción permite hacer una interpolación de los datos, obteniendo una riqueza esperada en un tamaño de muestra menor al tamaño que hemos logrado, de esta forma este proceso nos da no solamente la riqueza sino un error estándar. Si la muestra es un vector, la rarefacción se calculará para cada tamaño de la muestra por separado.

A continuación vamos a utilizar la función rarefy para construir las curvas de rarefacción basadas en individuos y en muestras.

2.1 Rarefacción basada en Individuos

Vamos a utilizar nuestros ya conocidos datos de BCI, a partir de estos datos realizaremos un submuestreo escogiendo 10 de las 50 parcelas de BCI, esto con el fin de simplificar el ejemplo.

Lo primero que necesitamos es obtener un vector (un objeto) con el total de individuos de cada especie, este objeto representa la comunidad sobre la que haremos la rarefacción y la estimación de la riqueza total. Queremos generar una curva parecida a la de acumulación de especies pero que nos dará una riqueza con el error estándar, para esto tenemos que definir en qué tamaños de muestra queremos hacer la interpolación. Vamos a realizar estos pasos en R.

#Usaremos los datos con los cuales construimos las curvas de acumulación
#Sumamos la abundancia de cada especie
N <- colSums(BCI_sub) 

#Hacemos un vector con los tamaños de muestra sobre los cuales haremos 
#la interpolación. El dato final de este vector es el tamaño total de la 
#muestra (sum(N))
subs3 <- c(seq(500, 4000, by = 500), sum(N)) 

#Ejecutamos la rarefacción
rar3 <- rarefy(N, sample = subs3, se = T, MARG = 2)
rar3

##           N500      N1000      N1500      N2000     N2500      N3000
## .S  106.511010 132.555792 146.508684 155.622094 162.27681 167.469582
## .se   4.615179   4.268649   3.873036   3.491962   3.09491   2.647784
##         N3500      N4000 N4276
## .S  171.69984 175.255907   177
## .se   2.09532   1.274649     0
## attr(,"Subsample")
## [1]  500 1000 1500 2000 2500 3000 3500 4000 4276

Como vemos el objeto rar3 nos muestra la cantidad de especies que se espera tener a diferentes tamaños de muestras, en el ejemplo desde 500 hasta 4296. En este caso en el tamaño de 500 se espera tener 108.32 especies con un error estándar de 4.63. La riqueza tiene decimales pues es la media de la aleatorización realizada.

2.2 Rarefacción basada en muestras

Para realizar una rarefacción basada en muestras utilizaremos los modelos de acumulación de especies de la función specaccum del paquete vegan. Utilizaremos el método “random” de esta función, que encuentra la riqueza de especies esperada para un tamaño de muestra.

rand<-specaccum(BCI_sub, method = "random", permutations=100)
rand

## Species Accumulation Curve
## Accumulation method: random, with 100 permutations
## Call: specaccum(comm = BCI_sub, method = "random", permutations = 100) 
## 
##                                                                    
## Sites     1.00000   2.00000   3.00000   4.00000   5.00000   6.00000
## Richness 92.57000 122.46000 137.97000 148.38000 155.91000 161.65000
## sd        6.66402   8.08593   6.61412   5.84787   5.27064   4.90593
##                                           
## Sites      7.00000   8.00000   9.00000  10
## Richness 166.26000 170.72000 174.21000 177
## sd         4.32661   3.49915   2.40914   0

En este caso lo que vemos es que con una sola muestra tendríamos 92.55 especies, con dos parcelas tendríamos 123.9 especies, y así sucesivamente como podemos ver aparentemente la curva tiende a estabilizarse a partir de la parcela 7.

2.3 Estimadores de Riqueza

Como vemos el efecto que tiene el esfuerzo de muestreo sobre la riqueza hace que medirla de forma exacta y precisa sea un tanto complejo. La comparación de la riqueza debería realizársela sólo a partir de inventarios completos (que han llegado a la asíntota de la curva de acumulación de especies), lo que generalmente es muy difícil de lograr con unos recursos limitados (ej. Longino et al 2002 muestra que después de 30 años de muestreo de hormigas en la estación La Selva en Costa Rica, no se ha logrado alcanzar la asíntota). Una buena opción para determinar la riqueza de una comunidad consiste en estimar el número de especies a partir de un muestreo previo.

Los estimadores de riqueza pueden ser paramétricos y no paramétricos

Muchos métodos de estimas de la riqueza han sido propuestos, pero las aproximaciones más utilizadas en ecología son mediante métodos paramétricos y no paramétricos (Colwell & Coddington, 1994). Los métodos paramétricos estiman el número de especies ajustando las abundancias de las especies a modelos de distribución paramétrica (series logarítmica, log-normal, o Poisson log-normal). En el caso de las aproximaciones no paramétricas se basan en el estudio de las especies raras y permiten estimar el número de nuevas especies a partir de las relaciones de abundancia o incidencia de las especies ya detectadas en el muestreo (González-Oreja et al. 2010).

Para estimar el número total de especies (riqueza asintótica) utilizaremos estimadores no-paramétricos. En primer lugar, utilizamos un estimador de riqueza basado en la abundancia el ACE, esta estimación la podemos hacer con la función estimateR que se encuentra en el paquete vegan. Además, utilizamos un estimador basado en la frecuencia de especies, Chao 2. Este estimador necesita datos de presencia/ausencia y múltiples parcelas de muestreo. Para esto utilizamos la función specpool.

#Utilizaremos el valor obtenido de la suma de todas las especies que obtuvimos previamente
ace <- estimateR(N)

#Podemos aplicar directamente sobre nuestra matriz y nos arroja un solo dato
chaoF <- specpool(BCI_sub) 
ace; chaoF

##      S.obs    S.chao1   se.chao1      S.ACE     se.ACE 
## 177.000000 197.312500  10.512240 193.287756   6.899095

##     Species  chao chao.se jack1 jack1.se    jack2     boot  boot.se  n
## All     177 193.8     8.4 202.2 10.69953 209.6667 189.6454 6.595226 10

Como vemos las dos funciones nos dan varios índices no únicamente el ACE y el Chao2. Según lo que creamos conveniente podemos utilizar cualquiera de ellos. El estimador ACE es bastante conservador y nos da una riqueza esperada de 196.08 con un error estándar de 6.83, mientras que Chao (de la función specpool) nos da una riqueza de 197.64 con una desviación de 6.63. En este caso el estimador Jacknife2 nos da la más alta riqueza con 213 especies.

2.4 Graficando los resultados

Ahora, graficamos las curvas de rarefacción basada en individuos y en muestras con su desviación estándar en los distintos tamaños de muestra escogidos, adicionalmente incluiremos los estimadores de riqueza y la riqueza total en las 50 ha del BCI.

par(mar=c(6,4,1,1))

#construimos el gráfico de rarefacción basada en individuos
plot(subs3, rar3[1, ], ylab = "Riqueza de especies", 
          axes = FALSE, xlab = "", cex.lab=0.8, 
        type = "l", ylim = c(50, 260), xlim = c(500, 7000), lwd=1.8)
points(subs3,rar3[1, ], pch=19)

#Graficamos la desviación estándar.
segments(subs3, rar3[1, ] + 2 * rar3[2, ], 
         subs3, rar3[1, ] - 2 * rar3[2, ])

#Graficamos los ejes
axis(1, at = 1:5 * 1000, cex.axis=0.7,mgp=c(3, 0.2, 0)) 
axis(2, cex.axis=0.7) 

#la caja
box() 

#Sobreponemos la curva de rarefacción basada en muestras
par(new=T)
#Hacemos un vector con el número de parcelas
x<- 1:10

#Graficamos la curva
plot(x, rand$richness, type="l", col="red",ylab="", xlab="", 
     axes=FALSE, xlim=c(1,15), ylim = c(50, 260), lwd=1.8)
points(rand$richness, pch=19, col="darkred")
segments(x, rand$richness + 2 * rand$sd, x, rand$richness - 2 * rand$sd, col="red")

#Graficamos la curva de acumulación
par(new=T)
plot(col, xlab="", ylab="", col="blue", axes=FALSE, xlim=c(1,15), 
     ylim = c(50, 260), lwd=1.8)
points(col$richness, pch=19, col="darkblue")

axis(1, at=1:10, cex.axis=0.7, line =3, mgp=c(3, 0.2, 0)) 

mtext("No. Individuos", side=1, line=1.3, cex=0.8, at=6)
mtext("No. Parcelas", side=1, line=4, cex=0.8, at=6)

legend(1, 250, c("Rarefacción - Muestras", "Curva de acumulación",
                 "Rarefacción - Individuos"), lty=c(1,1,1), pch=19,
       cex=0.7, col = c("red", "blue", "black"))

#Incluimos el estimador de riqueza ACE
points(11,ace["S.ACE"], pch=19)
segments(11, ace["S.ACE"] - 2 * ace["se.ACE"], 
         11, ace["S.ACE"] + 2 * ace["se.ACE"], lwd = 3) 

text(11, 160, "Estimador ACE", srt = 90, adj = c(1, + 0.5), cex=0.7)

#Incluimos el estimador de riqueza Chao2
points(12,chaoF[1, "chao"], pch=19, col="grey")
segments(12, chaoF[1, "chao"] - 2 * chaoF[1, 
                "chao.se"], 12, chaoF[1, "chao"] + 2 * chaoF[1,
                "chao.se"], lwd = 3, col = "grey") 
text(12, 160, "Estimador Chao2", srt = 90, adj = c(1, + 0.5), cex=0.7)

#La riqueza total de la parcela de 50ha del BCI

points(13, dim(BCI)[2], pch = 19, cex = 1) 
text(13, 160, "Riqueza  en 50 ha del BCI",
     srt = 90, adj = c(1, 0.5), cex=0.7)
text(13, 232, dim(BCI)[2], cex=0.6)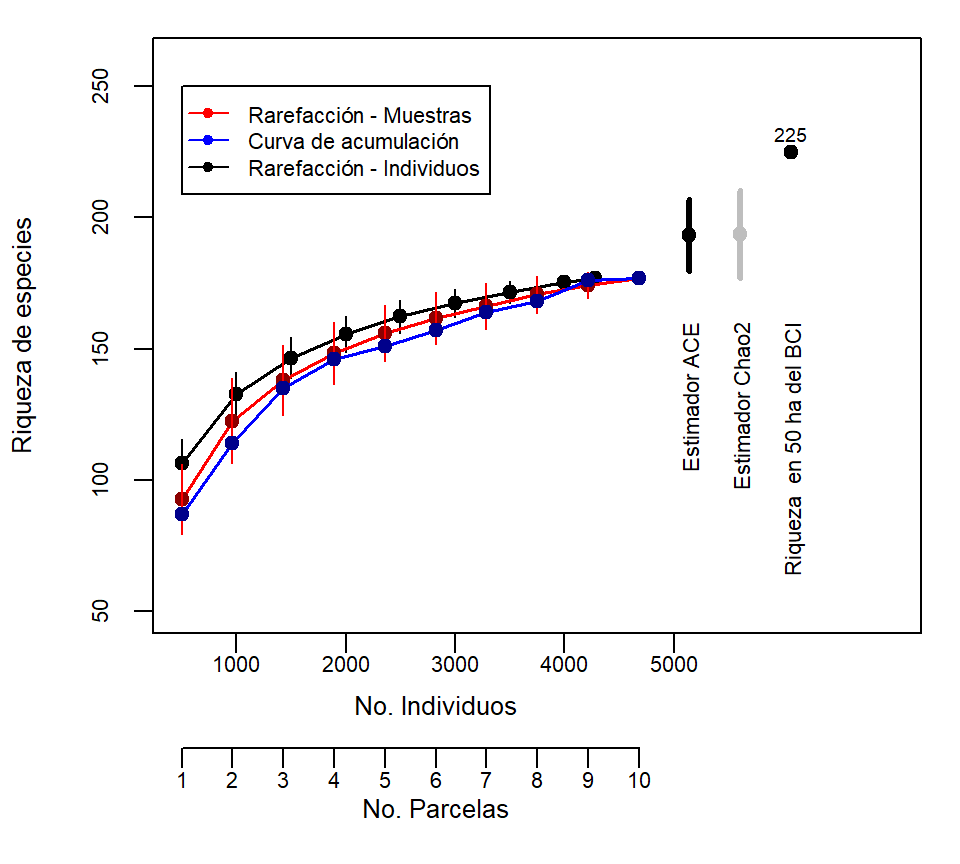

Figure 2.1: Curvas de rarefacción basada en individuos y en muestras de 10 parcelas al azar del BCI. Estimadores de riqueza (ACE) y Chao2 y riqueza total obtenida en las 50 ha del BCI.

En la figura 2.1 podemos ver que nuestro muestreo es aceptable y que aunque no hemos capturado toda la riqueza del área los estimadores que utilizamos son aceptables. Es posible que en este caso la riqueza de jacknife sea un mejor estimador. Pero recuerden que normalmente cuando hacemos un muestreo no tenemos el valor de riqueza total, por lo que no podemos saber cuan alejados estamos de la realidad.